Creationists would have us believe than nothing ordered can ever come from a random process. Of course, evolution is not a random process; it has random elements (mutations and sex), but also has elements that are the opposite of randomness (selection and heredity).

On this page, we consider the question "Can order arise from a completely random process?"

The answer is "Yes!" Read on...

 

DIGITAL DOODLES

by Dave Thomas : nmsrdaveATswcp.com (Help fight SPAM!  Please replace the AT with an @ )

[Originally printed in NMSR Reports, July 1996, Vol. 2, No. 7)]

The Sierpinski Gasket is a creationist's worst nightmare. Creationists often depict evolution as a random process with no hope of ever producing order. For example, John R. Doughty wrote in his thrice-printed letter to the Alb. Journal (June 2,5, and 6, 1996) that "The point is that everything including man was carefully designed, he and she (got to have both!) did not happen by random chance, mutant processes. Such processes lead to disorder, not order." And on Feb. 3, 1996, Doughty wrote in the Journal : "Without intelligent design, the chances of a complex, highly ordered system like the amoeba are the same as expecting a Boeing 747 to arise from a junkyard by itself after the passage of millions of years. The chance is nil."

Of course, Doughty is doing his best to ignore that most marvelous of organizing processes, natural selection. Perhaps I will cover how genetic algorithms can be used to "evolve" solutions to very difficult mathematics problems in a future column. For this essay, we will consider a random process that produces order without any type of "selection." The Sierpinski Gasket was developed by the Polish mathematician Waclaw Sierpinski (1882-1969). It is a fractal, with small portions of the shape appearing identical in structure to larger portions. There are several ways to produce the Gasket: some are deterministic methods (rule-based) and some are probabilistic (random). In §1, I'll show how to generate the shape with random methods. Then in §2, I'll use a deterministic approach to show how the random method actually works.

§1. Order from A Random Process

Take a piece of paper (or better yet, a computer screen), and place three points on it to define a triangle. The points don't have to be symmetrically placed. Then, pick a random point anywhere on the paper (screen). Now start picking random corners of the triangle. For example, you might roll a die, and assign the top corner to rolls of 1 or 6, the left corner to 2 or 5, and the right corner to 3 or 4. Whatever corner you picked, place a ruler between the corner and the point, measure half-way from point to corner, and place a new point at the half-way location. Repeat the process on the new point, and again on the next new point, and so on. After thousands of points, a curious shape will emerge, as shown in Figures 1 and 2.

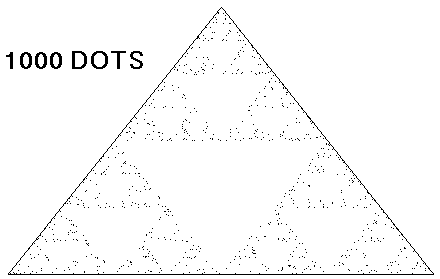
Figure 1.

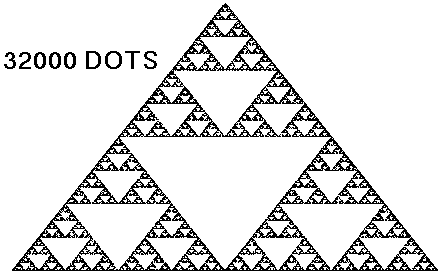
Figure 2.

Once of the most striking aspects of the shape in Fig. 2 is the presence of many white spaces (the inverted white triangles). Why do the random dots avoid these "forbidden zones?" How do they know where not to go?

Here is the entire listing of a program to draw shapes like these. This will work on older IBM PC-compatible computers. In DOS, type "QBASIC", type in the lines below, then hold the SHIFT key while you touch the F5 key to run the program. The listing is just 19 lines long, with a whopping total of around 390 keystrokes required.

----------------------------------------------------

DIM X0(3), Y0(3)
RANDOMIZE TIMER
XMIN = -.1: XMAX = 1.1
YMIN = -.1: YMAX = 1.1
X0(1) = 1/2: Y0(1) = 1
X0(2) = 0 : Y0(2) = 0
X0(3) = 1 : Y0(3) = 0
SCREEN 12
X = RND : Y = RND
DO
N = INT(3*RND) + 1
X = (X+X0(N))/2
Y = (Y+Y0(N))/2
XPC = INT(639*(X-XMIN)/(XMAX-XMIN))
YPC = INT(479*(YMAX-Y)/(YMAX-YMIN))
PSET (XPC,YPC), 9 + N
IF INKEY$ = CHR$(27) THEN STOP
LOOP
END
--------------------------------------------------

That's all there is to it! XO(N) and Y0(N) are arrays to hold the (x,y) coordinates of the three corners of the triangle. XMIN, YMIN, XMAX, and YMAX are plot limits for the display. The words RANDOMIZE TIMER start off the computer's random number generator with a new seed, providing different random values for each run. The "SCREEN 12" command sets up high-resolution graphics. The words "X=RND: Y=RND" assign random coordinates to the very first (x,y) point (RND will be a random number between 0.0 and 1.0). The lines between the words "DO" and "LOOP" are repeated until the ESCAPE key (ASCII code 27) is pressed. Inside the loop, the line N=INT(3*RND)+1 generates a random number of 1,2, or 3, for the first, second, or third corner of the overall triangle. The X and Y coordinates of the new point are obtained by calculating the average of the old X or Y coordinate and the X or Y coordinate of the randomly picked corner. This amounts to exactly the same thing as making the new point halfway to the corner from the old point. The formulas for XPC and YPC convert (x,y) coordinates to pixels for the PC screen. Give the listing to your creationist acquaintances with PCs - it'll drive them nuts! Better yet, give it to your kids, but don't tell them what it will do. It's easy to generate order from chaos! And to see just how chaotic this process really is, replace the words "PSET (XPC,YPC),9+N" with the words "LINE -(XPC,YPC),9+N". That leaves the pen "down" all the time. The next section, for the curious (and determined) reader, explores the question: how do the dots "know" to avoid the "white zones?"

§2. Provenance of the Gasket

To see how the fractal develops from random processes, we first need to see how it can be produced by intentional design. Let N be the "order" of various incarnations of the Sierpinski Gasket. An N = 0 gasket is simply a triangle, as shown below.

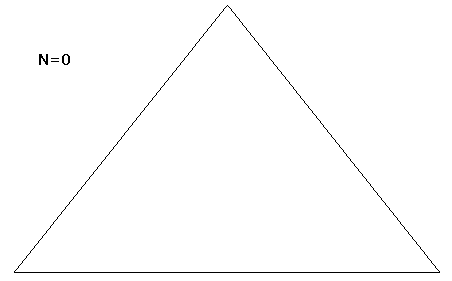
Figure 3. N = 0 Gasket

Now, starting with an order 0 shape, shrink it down to half the original dimensions (and thus one-fourth the original area), make two other copies of the new, smaller shape, and arrange the three small order 0 triangles to form a single full-sized order 1 triangle, as shown in Fig. 4.

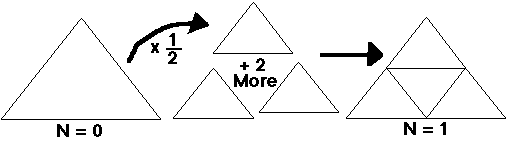
Figure 4. N = 1 Gasket

Then shrink the order 1 shape to half its size, combine it with two other copies to make an order 2 shape, and so on. Fig. 5 shows the creation of order 2, 3, and 4 shapes.

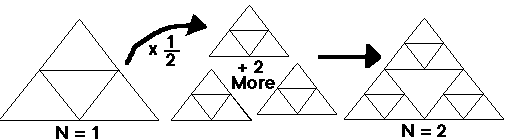
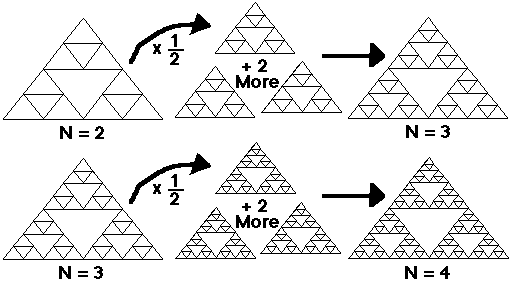
Figure 5. N = 2,3, and 4 Gaskets

Here's the rub. There is an amazing connection between the deterministic way of developing the gasket just described to the random process discussed earlier. It hinges on the relationship between points inside a full-sized triangle (which I'll call D, no matter what its order), and points inside the half-sized versions of D (which will be called D'). Examples of a D with order N=1, and a half-sized D' superimposed on the top half of D are shown in Figure 6. Here, while D' itself is of order N=1 (as is D also), three D' triangles together would make a new full-sized triangle D with N=2.

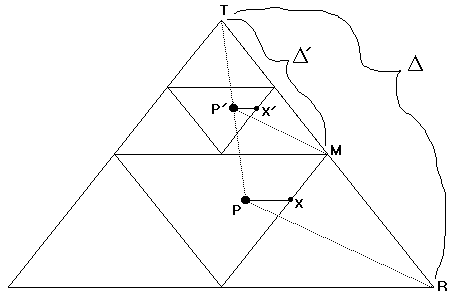
Figure 6. Full-sized (D) and Half-sized (D') Triangles

Now consider the point P in Fig. 6 above. P happens to be near the middle of the largest white space (forbidden zone), but it could be anywhere on the figure (even outside of the triangle). Now suppose we pick a random corner; in Fig. 6, the top corner (T) was chosen. Superimpose the small triangle D' over the randomly-picked corner of D. Now define an image point P' as that point which occupies the same position with respect to the half-sized gasket D' that point P does to the full-sized gasket D. Thus, point P' is also in the middle of a white space, but its white space is only half the size of the first white space (the one containing point P). Here is the amazing connection: P' , as just defined, is also THE point which would be obtained if you had started with P, randomly picked the top corner, and then moved half-way to that corner.

The proof isn't too difficult. It follows from similar triangles. First, by construction TM = TR / 2 , where TM indicates the distance from point T (top of triangle) to point M (along right side of triangle), and so on. This follows because D' is half the size of D. Then, TP' / TM = TP / TR by design (P' is to D' as P is to D). It follows directly that TP' = TP / 2, which is precisely the rule used for the random fractal.

It can be shown that the distance from P to any specified point (say, X) near the large gasket D is always twice the distance between the image point P' and the image of the specified point (say, X') near the small gasket D'. In other words, the distance from P' to X' is half the distance from P to X, or P'X' = PX / 2.

If you're still with me (and I'm proud of you if you are!), here's the payoff. In Fig. 7 below, I've started off with a point (labeled 1) in just about the worst possible location: right in the center of the largest white space. Let's follow this point through a few random iterations. Suppose we pick the top corner, and move halfway there (arriving at point 2). Note that point 2 is at the center of the largest white space in the upper half of the figure (the small triangle D'), but that this white space is half the size of the original (in the full-sized D). On the next try, we choose the lower left corner, and go half-way there, arriving at point 3. Note that point 3 occupies the same position with respect to the lower-left small triangle D' that point 2 does to the full-sized triangle D, and that 3's white space is half as small as 2's. For the next iteration, all three possible locations of the new image point 4 are shown. In fact, the three possible locations for 4 map out a perfect half-size triangle. Most importantly, the size of 4's white space is half that of 3's.

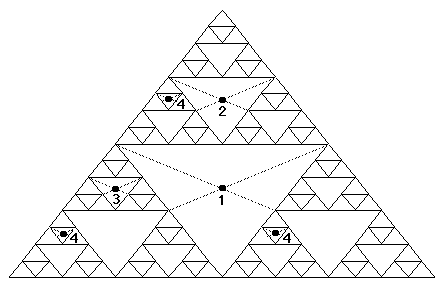
Figure 7. Follow the White Space Road

Clearly, the size of the enclosing white space is reduced by half with each iteration of the random process. In an ideal world, the point would always be in the middle of a white space, but the size of that white space would decrease exponentially. Once the enclosing white space decreases to the smallest size that can be resolved on the computer screen, however, the point will be indistinguishable from points which are not in white spaces (such as the corners of the given white space). For all intents and purposes, within 10 or so iterations, you will be plotting points that occur on the same pixel as points which are not in white spaces. And that is how points are driven away from the white zones. If you look carefully at the screen produced by the listing above, you may be able to see the first few iterations leaving points in white spaces - but only a few!

The randomness of picking corners ensures that an infinity of different points can be chosen. Although each point is related to the corresponding point of its parent fractal, the fact is that with one iteration, 3 new locations are possible; with 2 iterations, 9; with 3 iterations, 27; and so on. With the 1000th iteration, 3¹⁰⁰⁰ @ 10⁴⁷⁷ different locations are possible.

Here's an interesting fact: if you start at a valid corner point of an order N version of the gasket (such as points P or Q in Fig. 8, below), the next iteration will land you at corresponding valid corner points of an order N+1 shape. In Fig. 8, P and Q are valid points on an order N=3 gasket, while their images P' and Q' are valid points on an order N=4 gasket. These points again demonstrate how the image point P' is related to the small triangle D' just as P is related to the large triangle D. Note that for Q, because the same corner was picked twice in a row, the triangles D and D' are now smaller chunks of the full-sized triangle. Once you get to order 40 or so, the computer does not have enough precision to keep track of the point's "true" location. The point might even pop into a white space, but it would be a white space much, much smaller than the resolution of the screen, with the result again being the continuous avoidance of the larger (resolvable) white spaces.

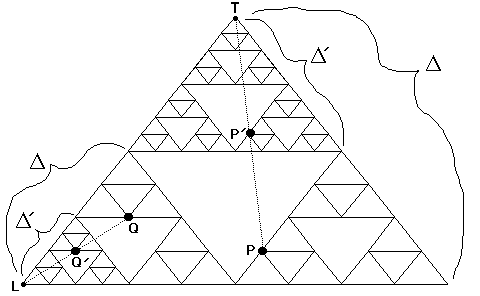
Figure 8. Initial Points at Corners

Order from Chaos?

Sure! Why not? This example shows not just that it happens, but how it happens as well.

  

Check out a cool Java Applet of the Gasket. It lets you draw with dots or with pen down (lines)!

http://www.shodor.org/MASTER/fractal/software/Sierpinski.html

  

NMSR Site Map