We STILL don't need no stinkin' Target!

ID Movement Still Stymied By Genetic Algorithms: War Of The Weasels Update
David E. Thomas
From: Skeptical Inquirer
Volume 44, No. 3
May / June 2020

Updated July 2nd, 2020

I last wrote about the “War of the Weasels,” the ongoing Creationist attacks on Evolutionary (Genetic) Algorithms, in the May/June 2010 issue of Skeptical Inquirer (Thomas 2010). Genetic Algorithms (GAs) are computerized simulations of evolution, and are used to study evolutionary processes, and also to solve difficult engineering or math problems. Intelligent Design (ID) Creationists often criticize these algorithms for not generating true novelty, and routinely claim that the “answer” is surreptitiously introduced into the program via the algorithm's fitness testing functions, or via “active information” surreptitiously added by the programmer. The example creationists always cite to prove that GAs must be spoon-fed their solutions is Richard Dawkins's “Weasel” simulation from The Blind Watchmaker (1986). This algorithm, used to show the power of cumulative selection, does include a precise description of its intended “Target,” the phrase “METHINKS IT IS LIKE A WEASEL” (Hamlet), which is used all through the execution of the procedure. However, Dawkins himself stated in his exposition that evolution itself does not have a goal or a target – unlike his “Weasel.”

In 2001, I set about to challenge this strawman argument by developing a Genetic Algorithm that solved problems without any knowledge of the answers in advance. I chose “Steiner's Problem”: given a two-dimensional set of points, what is the most compact network of straight-line segments that connects the points? (Additional “Steiner Points” besides the fixed points are allowed.) I presented this work at a lecture following a talk by Intelligent Design founder Phillip Johnson at UNM, and continued working on this problem thereafter.

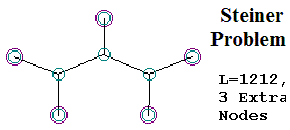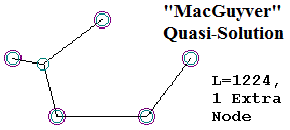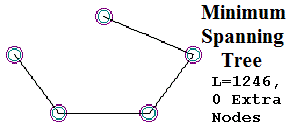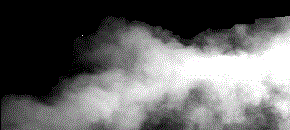
In the summer of 2006, I posted several articles on this topic on the Panda’s Thumb blog (Thomas 2006a). The series of posts culminated in a public “Design Challenge” (Thomas 2006b), in which readers were given a week to submit answers for a tricky six-point Steiner system. Because the ID crowd was saying the solutions were known beforehand, I posted all my source code, and challenged them to find the actual Steiner solution for the 6-point problem; it was an open-book test. Ironically, the ID “theorist” who was complaining the loudest, Salvador Cordova, was unable to derive the actual answer to the problem, even after many days of effort. The actual answers (two were possible) were found by my genetic algorithm in a few out of hundreds of runs, and also by dozens of independent fans of math and evolution. I was very surprised by the answers myself; I had expected a simpler solution, but this turned out to be inefficient. That’s why I chose this particular problem for the public “Design Challenge” in the first place: I didn’t know the actual answer, and could not possibly have “smuggled it in” (see Figure 1).

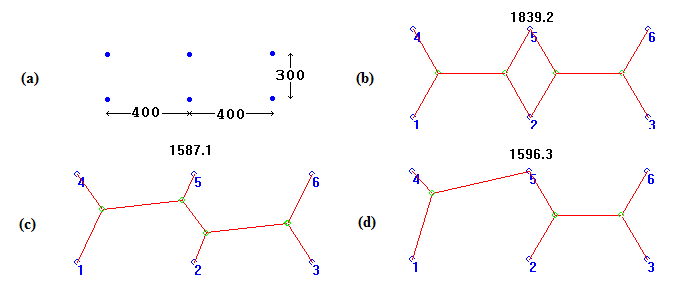
Figure 1: (a) The Design Challenge as posted on Panda’s Thumb; (b) the “Double Bowtie,” the shape the author expected as the solution to the challenge; (c) the actual best (Steiner) Solution, with a slightly twisted, but more minimal, arrangement of segments, and (d) a second-best “quasi” solution, which was the best that could be attained by ID theorists after weeks of effort. Because the actual Steiner shape was unknown to the programmer, there was no way the solution could have been added via“Active Information.”

So, after all these years, how has the ID community responded? The ID community has by and large ignored the point of the Steiner Challenge, which was simply that most Genetic Algorithms (Dawkins’ “Weasel” excluded) do not require the explicit answers it is hoped the algorithm will provide.

The mathematical stalwarts of the ID movement, William Dembski, Robert Marks and Winston Ewert (both still at Baylor, unlike Dembski, who was let go), have since responded to my article on the Steiner GA. Amazingly, they are all still painting all Genetic Algorithms with the “Weasel” brush, but any relevance to Dawkins or evolution science is becoming harder and harder to perceive.

The gist of the Ewert, Dembski and Marks response to the Steiner GA (Ewert et. al. 2012) is that “active information” is being supplied by the programmer to derive the answer. They say “The Darwinist claim is that no such assistance is required. Rather, natural selection is innately capable of solving any biological problem that it faces.” But that is clearly a strawman argument: have the stalwarts of ID never heard of … extinction?

In another paper published in 2014 in Biocomplexity, (Ewert 2014), Ewert attacks several GAs, including my Steiner algorithm. Ewert makes two huge errors in this part of his paper. He declares that the Steiner solutions are not “Irreducibly Complex”, because a different method of connecting points, the much simpler Minimum Spanning Tree (MST) algorithm, can easily connect the dots. He says “A connected network can be achieved by random chance alone. The difficulty in the Steiner tree problem is in trying to minimize the amount of road used, not in getting a connected network.” But the Steiner networks are not simple, and are clearly Irreducibly Complex: remove or alter any segment, and the network is no longer connected, as shown in Figure 2.

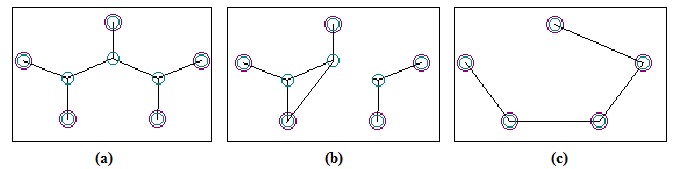
Figure 2. (a) This Steiner Solution for 5 Points is the actual Minimal Length Network. (b) This solution is Irreducibly Complex: if any segment is removed, or even re-routed, the connectivity becomes invalid. (c) A Minimum Spanning Tree for the same 5 Points; while this connects the points, it clearly does not have the complexity of the actual shortest network.

The second gaffe is use of the ID concept of “Specified Complex Information” (CSI). While the CSI concept is usually presented as “obvious” (the solutions must be complex, and specified as well), the mathematical definition of CSI has been carefully crafted so as to make the success of either evolution or GAs absolutely impossible. Dembski et. al. have defined CSI as the property of having “500 bits of complexity”. If the Genetic Algorithm under consideration always gets the answer to the posed problem, it thus has ZERO CSI (Dembski 2002). Even Dawkins’ “Methinks it is like a Weasel” has obvious complexity, but Dembski scores it as zero CSI, because the Dawkins algorithm always converges. If, like my Steiner algorithm, the GA does get the correct answer, say, only once in about 200 trials, it has less than 8 Bits of CSI (28 = 256). Only if the Genetic Algorithm gets the solution rarely (literally, once in 2500 ~ 10150 trials), does it finally achieve the honor of possessing “500 Bits of CSI.” This is as rare as tossing a fair coin 500 times, and getting heads every time. The Game is RIGGED: Neither Genetic Algorithms nor Evolution can ever create CSI! The creationist assault on GAs is interesting, but falls far, far short of the mark.

Dawkins, Richard. 1986. The Blind Watchmaker. New York: W.W. Norton and Company.

Dembski, W. 2002: No Free Lunch: Why Specified Complexity Cannot be Purchased Without Intelligence, Lanham, MD: Rowman & Littlefield.

Ewert, W. 2014: Digital irreducible complexity: A survey of irreducible complexity in computer simulations. BIO-Complexity1:1–10. doi:10.5048/BIO-C.2014.1. Available online here

Ewert, W., W. Dembski, Marks and R. J. Marks II, 2012. Climbing the Steiner tree— Sources of active information in a genetic algorithm for solving the Euclidean Steiner tree problem. BIO-Complexity 1: 1-14. doi:10.5048/BIO-C.2012.1. Available online here.

Thomas, David. 2006a. Target? TARGET? We don't need no stinkin' Target! Panda’s Thumb Blog (July 5). Available online here.

--------- 2006b. Design Challenge Results: Evolution is Smarter than You Are. Panda’s Thumb Blog (August 21). Available online here.

--------- 2010. The War Of The Weasels: Or How an Intelligent Design Theorist was Bested in a Public Math Competition by a Genetic Algorithm! Skeptical Inquirer 34(3) (May/June)

Target? TARGET? We STILL don't need no stinkin' Target! The War of the Weasels is back!
Updated January 5th, 2016.

by Dave Thomas : nmsrdaveATswcp.com (Help fight SPAM! Please replace the AT with an @ )

As part of the year-end Kitzmas festivities, The Discovery Institute's PR organ Evolution News and Views re-posted an earlier article titled Following Kitzmiller v. Dover, an Excellent Decade for Intelligent Design.

This uncredited article from September 2015 included the following, which caught my eye:
In fact, the decade since Dover has been an excellent one for ID. Casey Luskin noted some highlights not long ago:... Theoretical peer-reviewed papers taking down alleged computer simulations of evolution, showing that intelligent design is needed to produce new information.

The paper which was linked, hereafter Ewert 2014, is titled "Digital Irreducible Complexity: A Survey of Irreducible Complexity in Computer Simulations", and was written by Winston Ewert of the Biologic Institute for a 2014 edition of the institute's open-access journal BIO-Complexity.

Ewert claims that Michael Behe's concept of "Irreducible Complexity" is a stumbling block for evolutionary algorithms, and that several computer models of the evolution of irreducibly complex structures all fail to falsify Behe's concept. Ewert examines five models: Lenski's Avida, Schneider's Ev, my own Steiner Trees, Sadedin's Geometric Model, and Thompson's Digital Ears program.

I won't speak for the other models, but I can say this about Ewert's discussion of Steiner solutions to network problems: it's a massive strawman fallacy, a desperate "bait and switch" in which the problem my algorithm was solving, Steiner networks, was "replaced" with a much simpler problem, Minimum Spanning Trees. This ruse enabled Ewert to launch a (straw) attack on my genetic algorithm for solving Steiner's problem.

The Steiner Genetic Algorithm was the subject of a heated blog war, the "War of the Weasels," occurring between Panda's Thumb and Uncommon Descent during the summer of 2006. It all began with my post of July 5th, 2006, Target? TARGET? We don’t need no stinkin’ Target! It seemed the War of the Weasels ended in the fall of 2006, after Uncommon Descent's top programmers were unable to out-design the Steiner genetic algorithm during a public design challenge. But with Ewert's 2014 article, and an earlier 2012 piece in BIO-Complexity by Ewert, Dembski and Marks, it's clear that no ceasefire exists.

The War of the Weasels is back! More below the fold.

The "War of the Weasels" got its start with this post on PT. Why "Weasels"? Well, Richard Dawkins' 1987 book "The Blind Watchmaker" used a very simplified genetic algorithm to demonstrate that cumulative selection was much more powerful than random selection. Dawkins' demonstration involved comparing various strings to the known phrase from Shakespeare's "Hamlet," "Methinks it is like a weasel." Cumulative selection was demonstrated by basing the new "generation" of guesses for the phrase on the closest-matching member of the previous generation; in a few dozen generations, the target phrase was matched. By contrast, when random (e.g. no) selection was employed, the program floundered endlessly.

Even though Dawkins explicitly warned his readers that "Life isn’t like that. Evolution has no long-term goal. There is no long-distance target, no final perfection...", Dembski, Meyer and others consistently say that all genetic algorithms, just like Dawkins' "Weasel", must have the answers fed into the program -- if not explicitly, then surreptitiously via supplying "active information" or "front loading."

Both young-earth creationists and ID theorists attempt to smear all genetic algorithms using the "Weasel" brush. It's been that way for decades. To truly appreciate the depths to which the leaders of the ID movement are obsessed with Dawkins and "weasel," read Ian Musgrave's PT posts "Dembski Weasels Out" and "Weasles on Parade."

The purpose of my July 2006 PT "Target" post was to discuss a genetic algorithm I'd developed that solved a difficult math conundrum, "Steiner's Problem." For any arbitrary collection of n points, the Steiner solution is the minimum-length set of straight-line segments connecting the given points to each other, and to additional variable-position "interchange" points.

I picked Steiner's problem specifically to counter the "Weasel" charge that genetic algorithm answers were being fed into the programs. Because Steiner's problem applies to any configuration of points, I designed my program so that new configurations could be considered -- problems with no known answers. Imagine that.

The topic was the subject of a vigorous blog war in the summer of 2006, between Panda's Thumb and Uncommon Descent, culminating in the "Design Challenge." In that August 14, 2006 post, I challenged ID theorists and the general public to derive or devise the Steiner solution for six points arranged in a 3x2 rectangle; since the creationists were saying I was "front loading" the algorithm via my fitness function, I published that function, along with the complete program, and challenged them to reverse-engineer the solution. I knew it would be a good problem, because the solution my genetic algorithm came up with earlier truly surprised me. While Uncommon Descent's Salvador Cordova attempted to "design" the Steiner solution, he ended up falling short, coming up with only a "MacGyver" solution: a network that connects the given points with a short, but not the minimal network. It cannot be emphasized enough that so-called "MacGyver" solutions (named after the TV show "MacGyver", in which the hero would save the day using imperfect, klugy solutions to escape dangerous situations) are not "Steiner" solutions; they are simply imperfect networks that get close to the answer, but which do not achieve Steiner "perfection."

Several correct Steiner solutions, along with some creative MacGyver solutions, were submitted in the Design Challenge by non-ID contestants; some of these were designed, while others got the answer(s) from their own versions of a Steiner Genetic Algorithm. There's a road map to the summer's "War of the Weasels" in the summary post Genetic Algorithms for Uncommonly Dense Software Engineers. The upshot of it all was that Cordova and the Uncommon Descent software Team learned Leslie Orgel's aphorism the hard way: "Evolution is smarter than you are." Not one ID supporter could derive the solution which was obtained by multiple independent versions of a genetic algorithm for Steiner's problem.

The affair was also described in an article I wrote for the May-June 2010 issue of Skeptical Inquirer, "War of the Weasels: An Evolutionary Algorithm Beats Intelligent Design", Skept Inq 43:42–46 (PDF).

As mentioned above the fold, the paper Ewert 2014 caught my eye. Ewert's Figure 2 has a deceptive title, "A depiction of a Steiner tree." The network shown is a connected graph, and almost a "minimal spanning tree" as well, but it is most definitely not a Steiner Tree!

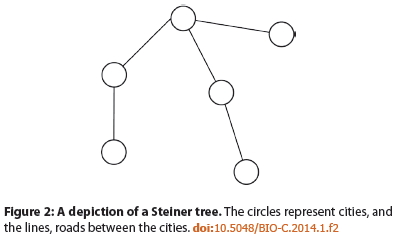
Ewert says the following about the Steiner algorithm:
Dave Thomas presented his model as a genetic algorithm that evolves solutions to the Steiner tree problem [Skept Inq 43:42–46.], a problem that can be viewed as how to connect a number of cities by a road network using as little road as possible. In his model Thomas penalizes excess roads and disconnected cities; the fitness function assesses a small penalty for each length of road and a large penalty for leaving any city disconnected. Thomas claims that his model can evolve an irreducibly complex system:
And finally, two pillars of ID theory, “irreducible complexity” and “complex specified information” were shown not to be beyond the capabilities of evolution. [Skept Inq 43:42–46]
He makes this claim because removal of any roads in Figure 2 disconnects the network, and makes it impossible to travel between some of the cities. According to Thomas, the roads are therefore the parts of an irreducibly complex system. It should be noted, however, that obtaining a connected road network is actually trivial—a connected network can be achieved by random chance alone. A depiction of such a network can be seen in Figure 2. The difficulty in the Steiner tree problem is in trying to minimize the amount of road used [EDM 2012], not in getting a connected network. Therefore we can say that there are no intermediate evolutionary stages in obtaining such a network.

This is the bait and switch. True Steiner solutions are not only Irreducibly Complex, they have Complex Specified Information, as they are specific solutions of an NP-hard math problem. But Ewert simply discards the requirement that the network be minimal length, and substitutes a far easier problem, Minimum Spanning Trees. Since random chance selections can happen upon Minimal Spanning Trees fairly easily, Ewert says the solutions are thus trivial, and thus not really "irreducibly complex" as per Behe's concept.

Ewert refers to an earlier 2012 paper he wrote along with William Dembski and Robert J. Marks II, Climbing the Steiner tree—Sources of active information in a genetic algorithm for solving the Euclidean Steiner tree problem. BIO-Complexity 2012(1):1-14, hereafter EDM 2012. This paper has some of the same errors as the newer one, and some additional whoppers as well. As in the later paper, EDM find ways to rationalize the Steiner Problem into the Minimum Spanning Tree problem, and attack the latter, a classic strawman fallacy. In the process, EDM omit key solutions, and misrepresent others.

One whopper occurs on the second page, when EDM deride the problem-solving capability of genetic algorithms, and say that all such programs need "assistance" with their searches. Then EDM say "The Darwinist claim is that no such assistance is required. Rather, natural selection is innately capable of solving any biological problem that it faces."

As pointed out by the Skeptical Zone in a review of EDM 2012, "No 'Darwinist' (a term that reflects ID's creationist roots) claims this. Extinction is known to happen."

The worst flaw in EDM comes around their Figures 3 and 4, where the authors perform the switch of the actual Steiner problem with the much simpler Minimum Spanning Tree problem. Here is EDM's Figure 3, which applies to the 5-point Steiner problem discussed on PT during the summer of 2006.

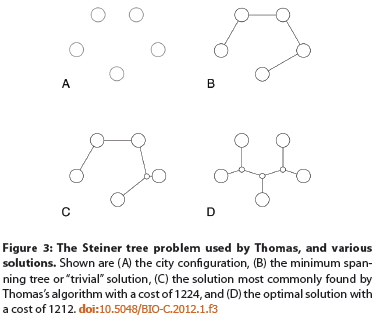
The Fix is in with EDM's Figure 3, but it's not apparent unless you can see the actual shapes EDM are discussing, taken directly from the We don’t need no stinkin’ Target! opening post in the blog war. These are reproduced below. What are the errors? First, EDM's Figure 3 completely omits the "Best MacGyver" shape with a length of 1217; in fact, this key solution appears nowhere in EDM 2012, with the exception of an un-labeled graph point in their Figure 4. EDM's Fig. 3 does include the "2nd-Best MacGyver" shape with a length of 1224, the "Minimum Spanning Tree" solution with a length of 1246, and the Steiner Solution itself (labeled simply "optimal solution"), with a minimum path length of 1212.

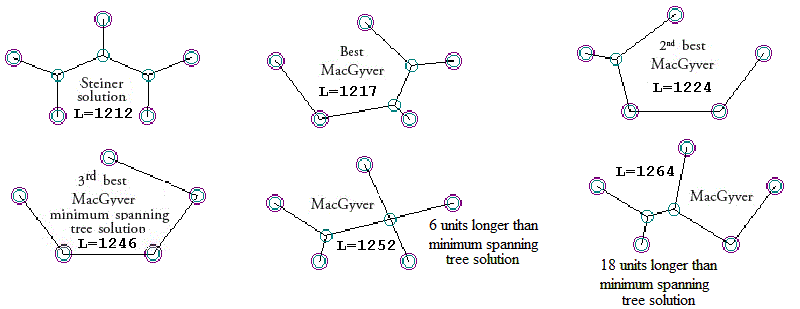
Smoke and Mirrors are used to even greater lengths two pages after EDM's Fig. 3; a portion of page 6 appears below.

In the passage above, EDM make math mistakes on the order of "1246 < 1217; 1246 < 1224". EDM say that the "MacGyver" solutions for the five-point problem are "more expensive" (longer) than the "minimum spanning tree solution." As the shapes from the original "Target" post" show, however, EDM are so obsessed with trying to downgrade the Steiner problem into the Minimum Spanning Tree problem, they somehow convinced themselves that the Minimum Spanning Tree is second only to the Steiner, and better (shorter) than the "MacGyvers." This is astonishing, because in their Figure 3, EDM displayed one of these MacGyvers (2nd-best MacGyver, with a length of 1224), which is greater than the Steiner (length 1212) but much shorter than the Minimum Spanning Tree, with its length of 1246. Curiously, the Minimum Spanning Tree was displayed in EDM's Figure 3, but its greater length, 1246, was omitted from the figure. It is acknowledged elsewhere in EDM's text. Not so for the "Best MacGyver" of length 1217; this is implied in EDM's Figure 4, but not drawn or referenced explicitly anywhere in EDM 2012. When EDM say "the other two (MacGyver) solutions... are more expensive", they are painfully, obviously wrong. The 1st and 2nd MacGyvers were less expensive than the Minimum Spanning Tree. I also showed two MacGyver solutions that were longer than the Minimum Spanning Tree (1252, 1264), but that doesn't help EDM. EDM simply ignored the 1st MacGyver (length 1217) and misrepresented the 2nd MacGyver (length 1224), and declared that both were of length more than 1246.

Are EDM wrong? Of course. It's as easy as "1217 exists, and it's less than 1246. 1224 is also less than 1246."

More smoke and mirrors are employed in EDM's Figure 4, which compares genetic algorithm results to random queries.

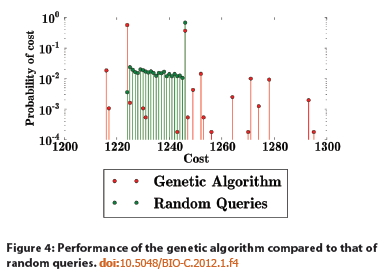
I have annotated their diagram with stick figures showing the horizontal coordinates (lengths, with 1212 being the Steiner solution) and MacGyver (NON-STEINER) solutions they are discussing, as well as the elephant in the Room: the actual Steiner Solution itself, which was omitted completely from EDM's Figure 4! (Lower left in the annotated figure.)

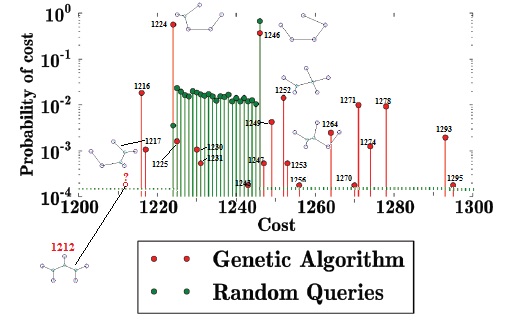
EDM spend most of their efforts justifying switching the actual problem with a much simpler one. While the actual Steiner Solution for the 5-points-in-a-pentagon problem requires three additional "interchange" points, EDM dismiss the importance of interchanges. Perhaps they think that if there is one fixed interchange in the 5-point problem, then that can be treated as finding the minimum spanning tree for a six-point problem? Don't they realize that the positions of interchanges is as critical as the number of such interchanges? Why did they pick the one position for their "interchange" point which was shown to be successful by my genetic algorithm? EDM's confusing and tortured arguments fill the air with smoke, which, as it dissipates, reveals only one conclusion:
Repeated random queries will quickly find the minimum spanning tree with high probability. As a result, having a search algorithm find it is no great success.
The smoke and mirrors are revealed! This is the subtle "bait and switch" whereby EDM turn the truly difficult Steiner Problem into the boringly trivial Minimum Spanning Tree problem.

EDM 2012 has pages and pages of "cargo-cult science" charts and equations, but falls short on actual substance. They make a big point of how my algorithm pre-located interchanges more in the center, and that this was introducing "active information." What they overlooked, however, was that this was a feature of the slow FORTRAN version only, and was removed (as quite un-necessary) in the much faster C++ version. If anything, EDM inadvertently showed genetic algorithms can get by with less active information!

Upon looking at the 6-point figure used in both Ewert 2014 and EDM 2012, I realized that EDM were clueless about the nature of Steiner solutions, and so I set out to find out what the real Steiner Tree looked like for the connected graph used by Ewert et.al. I digitized the points in Ewert's tree, and fed them into my Steiner genetic algorithm, and sat back awaiting the results. After a few minutes, my suspicions were proved correct: the EDM 6-point "minimal spanning tree" wasn't even a minimal spanning tree, but rather just a lowly connected graph. And, the other MacGyvers that came out of the algorithm were all "less expensive" than the EDM figure.

Steiner Algorithm results appear below. Starting at the upper left, EDM's supposed "Steiner" is 132 units longer than the actual Steiner Solution (bottom right, length of 1575 units), and over 60 units longer than the actual "Minimum Spanning Tree" (middle top, length = 1642 units). The remaining three MacGyver solutions are all less expensive than the Minimum Spanning Tree (lengths of ~1595, 1592, and 1588). The supposed "Steiner Tree" iconically displayed in both Ewert 2014 and EDM 2012 is not a Steiner tree; it isn't even the "Minimum Spanning Tree" for those 6 points! This is truly a pathetic spectacle.

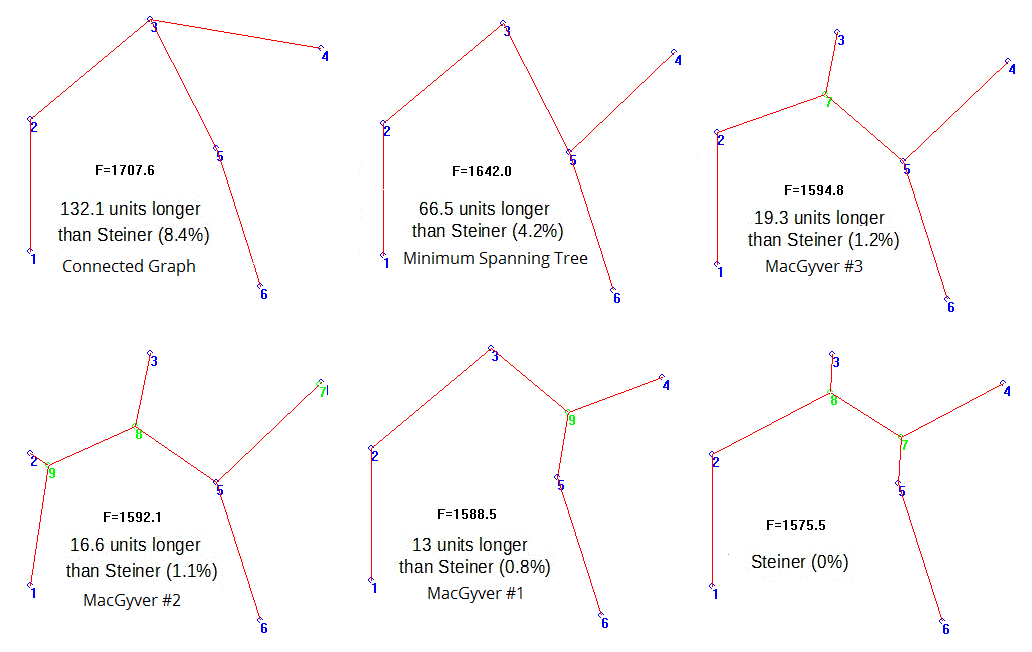
In the end, EDM have only wisps of smoke to show for all their efforts. The Steiner Genetic Algorithm remains an effective demonstration that genetic algorithms can produce irreducibly-complex, specified-information solutions of problems with no known answers.

We STILL don't need no stinkin' Target!