New Mexicans for Science and Reason present
NMSR 9-11 'Truth' Resources
How Does a Building Crush Itself?
By Dave Thomas

New Mexicans for Science and Reason present
NMSR 9-11 'Truth' Resources
How Does a Building Crush Itself?
By Dave Thomas

One of the most frequent assertions of the 9/11 "Truth" movement is that the structural steel columns of the Twin Towers would have resisted being crushed by the falling upper sections. Richard Gage says that one of the characteristics of destruction by explosives is that "Destruction proceeds through the path of greatest resistance at nearly free-fall acceleration."
This article presents part of the basic physics of such phenomena (continued in the next two articles), and shows that, for each tower, the first and subsequent impacts from the falling upper sections exceeded design safety margins by at least a factor of thirty. Strong as the towers were, they never had a chance against large falling sections of upper sections of the towers, moving at 20 miles per hour or greater.
The Twin Towers used the "tube within a tube" architectural design. A dense grouping of thick central columns formed the core, and provided vertical support. The perimeter walls provided both vertical and horizontal support. The central core was connected to the perimeter walls by the floors themselves, and by the hat truss on top of the buildings.
| The Core and Perimeter Walls | 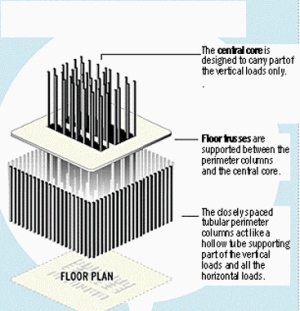 |
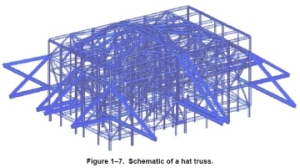 | The Hat Truss |
| The Towers were Mostly Air Inside |  |
The mainstream scientific consensus - what Truthers dismiss as the "Official Story" or "Official Conspiracy Theory" - has converged on a well-supported explanation of the towers' collapses. The key points of this explanation are that the planes started fires when they slammed into the towers, each carrying about 10,000 gallons of jet fuel, and going at hundreds of miles per hour. Several support columns were cut by the airplane impacts, but the hat truss was able to redistribute loads to the perimeter walls, and keep the buildings standing for a while. The fires weren't hot enough to melt the steel support beams and trusses, but did soften the trusses enought to where they sagged, and pulled inward on the perimeter walls.
 | More on the sagging trusses at debunking911.com |
| The perimeter walls were gradually pulled inward, until they snapped under the strain. This gradual process is not a feature of any controlled demolition. |  |
Once the perimeter walls snapped, the buildings were no longer capable of supporting the upper sections, and these began to fall. The mainstream view is that the large masses of these upper sections of the towers (about 14 floors for World Trade Center 1, and around 30 for WTC 2) became unstoppable by the time they had fallen the height of one floor (12 feet, or about 3.8 meters), initiating an "inevitable" progressive collapse of each building.
 | Critics like Richard Gage have cried foul. In the Roberts/Gage Hardfire debate, Gage drops two small boxes, one on empty air, and the second on a 30-inch tall sturdy cardboard box. (24 minutes in) Gage says "The one that had no resistance under it falls at freefall speed …. The one that has 80,000 tons of structural steel on it - it doesn't even give. It resists. As met by an equal and opposite reaction known as the conservation of momentum. It doesn't fall." |
More recently, Gage's website, Archbitects and Engineers for 9/11 Truth, has said of the model presented here that "Thomas, like others who debate Gage, relies on the 'Piledriver Theory' to explain how the smaller top section of the towers could destroy everything under them. The theory says that a structural failure due to fires caused the top section to drop one floor, which set off a chain reaction that completely demolished the buildings. The dynamic force simply overwhelms the building structure below. Gage notes that his theory ignores the structural resistance supplied by about 300 massive columns in the building."
This isn't true at all. I take full acount of the columns and other supports sing the approach outlined in Why Did the World Trade Center Collapse?—Simple Analysis" by Bazant and Zhou: "... one may estimate that C ~ 71 GN/m ..."
That means the towers acted like an extremely stiff spring because of their support structures. How stiff? So stiff, that the entire weight of the upper section (14 floors) would compress the supporting floor's 300 columns by just 8 millimeters - or about a third of an inch. (The mass of the upper part of the North Tower, WTC1, was on the order of 58x106 kg. The deflection of the "spring" is force divided by spring constant, i.e. 58 million kg, times g, divided by 71x109 nt/m.)
Those are some pretty stiff support structures! Here's how applied physics can use the stiffness of these structures to find the actual dynamic force imparted when the upper sections of the towers fell onto the lower sections below.
| The Spring Force Equation. The force required to compress the spring a distance x is proportional to the distance, and to the spring's stiffness, K: | 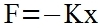 |
| The Energy stored in the spring is the integral of Force, F, over a given Distance, x: | 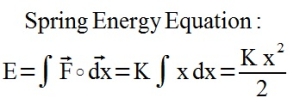 |
| The Spring Energy Equation: potential energy (mgh) converted to spring compression, where h is the height that the dropping mass falls, m is its mass, and g is the acceleration of gravity (9.8 m/sec2): | 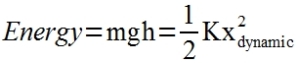 |
| Solving for xdynamic2: | 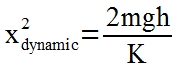 |
| The dynamic force is then: | 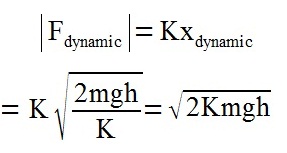 |
| Recapping, the dynamic force is : | 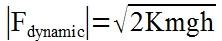 |
We tested this equation using a small spring scale, with a spring constant of about 60 nt/m. We dropped several different kinds of masses on it, from spherical ball bearings, to cylindrical nickels, to loosely-wrapped bags of rice. But, the reactions happened too fast to see, so we got the help of the high-speed camera operated by Professor Richard Sonnenfeld of New Mexico Tech Physics Department, and found out how hard the masses were impacting the scale.
Here's how the experiments turned out.
| The rice was loosely wrapped in some flimsy mesh used for rice packets at weddings, to investigate the impacts of objects which themselves are not stiff or tightly bound. We did this to learn about impacts of objects which may consist of a loose assortment of materials. |  |
| The rice packet has a mass of 4.8 grams, and a weight of about 0.17 oz, when measured at rest (static). |  |
| The important thing is that if we know the mass of a falling object, the height it falls, and the stiffness of the structure it impacts, we can estimate the dynamic force on that structure. For the known stiffness (Spring Constant, 60 nt/m), Rice Mass (4.8 gm), and Drop Height (2 to 16 inches), the theoretical curve is a parabola. The dynamic force increases as the square root of the drop height. To increase the force by two, the height is increased by four times. Here, the ratio of dynamic to static force is shown. | 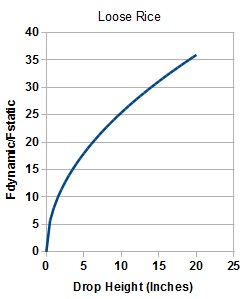 |
| The high-speed camera was used to record the point of maximum deflection, which was used to find the dynamic force.The dynamic force increased just as had been predicted. Here it is for a drop height of two inches: | 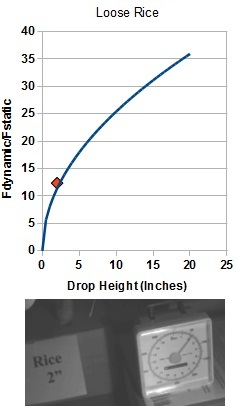 |
| Here it is for a drop height of four inches: | 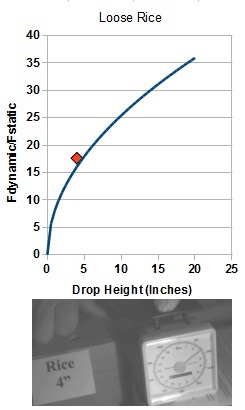 |
| Here it is for a drop height of nine inches: | 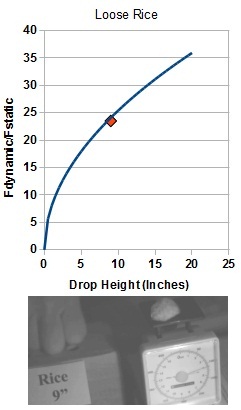 |
| Here it is for a drop height of sixteen inches: | 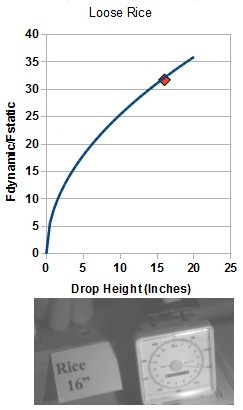 |
| Now, this equation provides estimates of dynamic force for objects of known mass, falling from known heights, and impacting on objects of known stiffness. For the massive North Tower, the mass was 58x106 kg (top 14 floors), the stiffness 71x109 nt/m, and the drop height was 3.8 meters. |  |
| The bottom line, for the top section of the North Tower impacting the 95th floor after the failure of the 96th floor: |  |
Here's the thing: this calculation indeed takes into account the stiffness of the towers and their horizontal floor supports. Yet, we see that the force of the upper section of tower impacting on the bottom section was about 31 times the static force - the normal weight of the upper section, at rest.
Buildings are designed to be stronger than needed, so as to be able to endure wind, earthquakes, and so on. Usually, having the building able to withstand loads a factor of three to five times the actual (static) load is considered adequate for safety. The first floor is simply overwhelmed with a force of 31 times the static load. But, what are the next floors hit with? That requires consideration of velocity.
| For floors after the first one that was impacted, the falling mass has more energy than that which was gained falling through one floor height. Now, velocity should be used. Here, kinetic energy is equated with spring compression energy. | 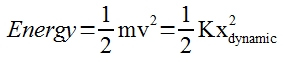 |
| Solving for xdynamic2: | 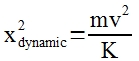 |
| The dynamic force is then: | 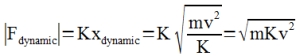 |
| Recapping, the dynamic force is : |  |
| After the failure of the 95th floor, the 94th floor is hit by a section of tower having 62 million kg mass, and a velocity of 11.8 meters per second (as found here). | 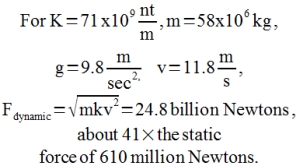 |
The next article in this series derives velocities of the collapses, using conservation of momentum. When these velocities are used to find the dynamic forces on each floor in turn, the accelerations are found to vary from 31 g's (1st impact), 41 g's (2nd impact), 47 g's (3rd impact), and increasing up to around 67 g's.
The fact is, when that first floor failed, and the upper section fell on the lower part of each tower, the huge forces, always greater than 30 times the static loads, would have overwhelmed every floor in turn, leading to progressive collapse. That's why the collapse was "inevitable" - and that's how a building can, indeed, crush itself.
It's important to realize that this process does not necessarily "break" the horizontal floor supports. We know that the perimeter walls peeled off to the sides, and also that tottering remnants of the core columns - the "Spires" - did not fall until several seconds after the main collapse. What was breaking at each impact were the connections of the floors to the horizontal floor supports. The floors themselves were quickly pulverized by the tremendous energy of the collapses.
| The "Spires", the tottering remnants of the central core columns. |  |
| Another view of the "Spires". |  |
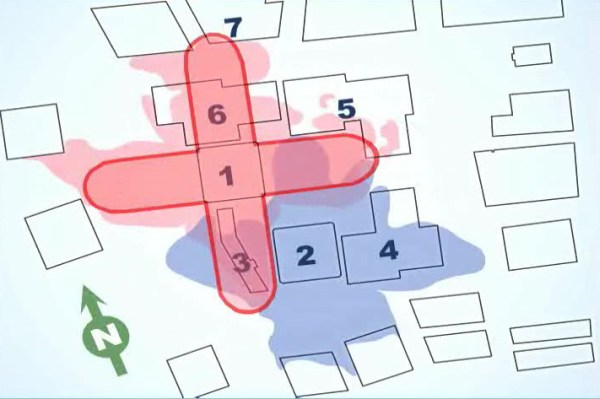
Richard Gage says the Twin Towers showed "Improbable symmetry of debris distribution," and describes this as one of the "characteristics of destruction by explosives." He is wrong. The firm Weidlinger Associates Inc. (WAI) was hired by the ownwers of the WTC to determine if the tower collapses were one or two insurable "events." If Tower 1 was toppled over by Tower 2, for example, the insurance company would pay for only one event. If the collapses were independent, however, two events would have to be covered. WAI, in their detailed analysis titled "World Trade Center - Structural Engineering Investigation," produced detailed maps of the debris distribution. Because the perimeter walls peeled off from the walls along the four sides of each building, there was a natural 4-leaf-clover pattern to the debris pileups. But, there was significant asymmetry. Where a tower leaned over a bit during the collapse, debris was pushed farther from the towers. Also, the debris footprint of Tower 1 is 20 to 25% larger than that for tower two, because one plane hit Tower 1 near the 96th floor, while Tower 2 was hit around the 80th floor. Tower 1's debris had farther to fall, and logically was spread out wider. Incidentally, the reason Tower 2 collapsed first is that the greater mass of the upper section above the plane impact floors put more load on the stressed structure, making it fail quicker.
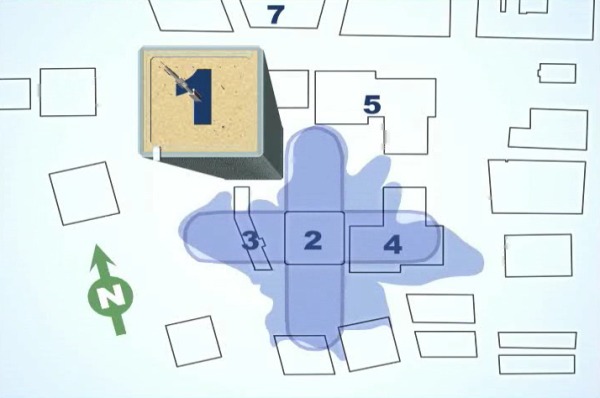
Note the lack of debris distribution symmetry, for both South (above) and North (below) Towers.
The main point of this article is that as the upper sections, composed of a given number of floors, impacted the lower portions of the buildings, floors were broken quickly by the 30-to-70-times-static-weight of the impacts, becoming part of the growing mass of the upper section. This fact will be used in the next article of this series, which looks at each impact as the inelastic* collision of an upper section of N floors with just one floor of the lower section. This approach is reasonable because each floor was broken one at a time, joining with the growing mass as it became a juggernaut of destruction.
*In an inelastic collision, the two colliding objects stick together.
Most people can hold a 50-pound bag of rocks, However, the impact of that same bag, dropped from 12 feet up, would almost certainly be lethal.
The third article in this series looks at the biggest mistake of Truth movement physics: the 100-times-too-low calculation of dynamic force.

NMSR 9-11 'Truth' Resources
How Does a Building Crush Itself?
The Towers' Collapse: Fast, But Not Freefall
Chandler's Data Support a Gravitational Collapse!
World Trade Center 7 : What Really Happened
How Can Gravity cause Multi-ton steel sections to be ejected laterally?
Is Thermite the Answer? What was the Question?
The Gage Page - "Blueprint of Destruction" Refutations
Main 9/11 Page
